Coherent risk measure

In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function ρ that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.

Properties

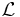Consider a random outcome $X$ viewed as an element of a linear space $\mathcal{L}$ of measurable functions, defined on an appropriate probability space. A functional 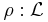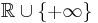$\rho�: \mathcal{L}$ → $\R \cup \{%2B\infty\}$ is said to be coherent risk measure for 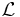$\mathcal{L}$ if it satisfies the following properties:^[1]

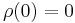
Normalized: $\rho(0) = 0$

That is, the risk of holding no assets is zero.

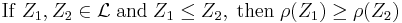
Monotonicity: $\mathrm{If}\; Z_1,Z_2 \in \mathcal{L} \;\mathrm{and}\; Z_1 \leq Z_2 ,\; \mathrm{then} \; \rho(Z_1) \geq \rho(Z_2)$

That is, if portfolio 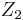$Z_2$ always has better values than portfolio 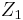$Z_1$ under all scenarios then the risk of 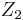$Z_2$ should be less than the risk of 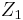$Z_1$ .^[2]

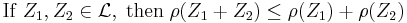
Sub-additivity: $\mathrm{If}\; Z_1,Z_2 \in \mathcal{L} ,\; \mathrm{then}\; \rho(Z_1 %2B Z_2) \leq \rho(Z_1) %2B \rho(Z_2)$

Indeed, the risk of two portfolios together cannot get any worse than adding the two risks separately: this is the diversification principle.

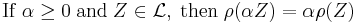
Positive homogeneity: $\mathrm{If}\; \alpha \ge 0 \; \mathrm{and} \; Z \in \mathcal{L} ,\; \mathrm{then} \; \rho(\alpha Z) = \alpha \rho(Z)$

Loosely speaking, if you double your portfolio then you double your risk.

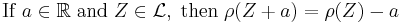
Translation invariance: $\mathrm{If}\; a \in \mathbb{R} \; \mathrm{and} \; Z \in \mathcal{L} ,\;\mathrm{then}\; \rho(Z %2B a) = \rho(Z) - a$

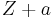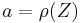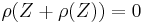The value $a$ is just adding cash to your portfolio $Z$ , which acts like an insurance: the risk of $Z%2Ba$ is less than the risk of $Z$ , and the difference is exactly the added cash $a$ . In particular, if $a=\rho(Z)$ then $\rho(Z%2B\rho(Z))=0$ .

Convex risk measures

The notion of coherence has been subsequently relaxed. Indeed, the notions of Sub-additivity and Positive Homogeneity can be replaced by the notion of convexity:^[3]

Convexity: $If \ Z_1,Z_2 \in \mathcal{L}\text{ and }\lambda \in [0,1] \text{ then }\rho(\lambda Z_1 %2B (1-\lambda) Z_2) \leq \lambda \rho(Z_1) %2B (1-\lambda) \rho(Z_2)$

Examples

Value at risk

It is well known that value at risk is not, in general, a coherent risk measure as it does not respect the sub-additivity property. An immediate consequence is that value at risk might discourage diversification.

Value at risk is, however, coherent, under the assumption of elliptically distributed losses (e.g. normally distributed) when the portfolio value is a linear function of the asset prices. However, in this case the value at risk becomes equivalent to a mean-variance approach where the risk of a portfolio is measured by the variance of the portfolio's return.

Illustration

As a simple example to demonstrate the non-coherence of value-at-risk consider looking at the VaR of a portfolio at 95% confidence over the next year of two default-able zero coupon bonds that mature in 1 years time denominated in our numeraire currency.

Assume the following:

The current yield on the two bonds is 0%
The two bonds are from different issuers
Each bonds has a 4% probability of defaulting over the next year
The event of default in either bond is independent of the other
Upon default the bonds have a recovery rate of 30%

Under these conditions the 95% VaR for holding either of the bonds is 0% since the probability of default is less than 5%. However if we held a portfolio that consisted of 50% of each bond by value then the 95% VaR is 35% since the probability of at least one of the bonds defaulting is 7.84% which exceeds 5%. This violates the sub-additivity property showing that VaR is not a coherent risk measure.

Average value at risk

The average value at risk (sometimes called expected shortfall or conditional value-at-risk) is a coherent risk measure, even though it is derived from Value at Risk which is not.

Tail value at risk

The tail value at risk (or tail conditional expectation) is a coherent risk measure only when the underlying distribution is continuous.

Entropic risk measure

The entropic risk measure is a convex risk measure which is not coherent. It is related to the exponential utility.

Superhedging price

The superhedging price is a coherent risk measure.

Set-valued

In a situation with 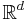$\mathbb{R}^d$ -valued portfolios such that risk can be measured in 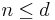$n \leq d$ of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costs.^[4]

Properties

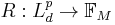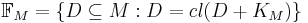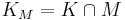A set-valued coherent risk measure is a function $R: L_d^p \rightarrow \mathbb{F}_M$ , where $\mathbb{F}_M = \{D \subseteq M: D = cl (D %2B K_M)\}$ and $K_M = K \cap M$ where $K$ is a constant solvency cone and $M$ is the set of portfolios of the $m$ reference assets. $R$ must have the following properties:^[5]

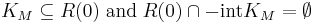
Normalized: $K_M \subseteq R(0) \; \mathrm{and} \; R(0) \cap -\mathrm{int}K_M = \emptyset$

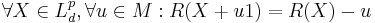
Translative in M: $\forall X \in L_d^p, \forall u \in M: R(X %2B u1) = R(X) - u$

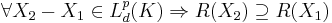
Monotone: $\forall X_2 - X_1 \in L_d^p(K) \Rightarrow R(X_2) \supseteq R(X_1)$

Sublinear

Set-valued convex risk measure

If instead of the sublinear property,R is convex, then R is a set-valued convex risk measure.

Relation to Acceptance Sets

An acceptance set is convex (coherent) if and only if the corresponding risk measure is convex (coherent). As defined below it can be shown that 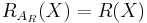$R_{A_R}(X) = R(X)$ and $A_{R_A} = A$ .

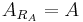Risk Measure to Acceptance Set

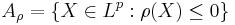If $\rho$ is a (scalar) risk measure then $A_{\rho} = \{X \in L^p: \rho(X) \leq 0\}$ is an acceptance set.
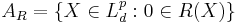If $R$ is a set-valued risk measure then $A_R = \{X \in L^p_d: 0 \in R(X)\}$ is an acceptance set.

Acceptance Set to Risk Measure

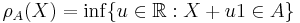If $A$ is an acceptance set (in 1-d) then $\rho_A(X) = \inf\{u \in \mathbb{R}: X %2B u1 \in A\}$ defines a (scalar) risk measure.
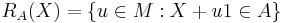If $A$ is an acceptance set then $R_A(X) = \{u \in M: X %2B u1 \in A\}$ is a set-valued risk measure.

Dual representation

A convex risk measure $\rho$ can be represented as

$\rho(X) = \sup_{Q \in \mathcal{M}_1} \{E^Q[-X] - \alpha(Q)\}$

such that $\alpha$ is a penalty function.

A risk measure is coherent if and only if it can be represented as

$\rho(X) = \sup_{Q \in \mathcal{Q}} E^Q[-X]$

such that 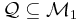$\mathcal{Q} \subseteq \mathcal{M}_1$ .^[6]

Relation to deviation risk measure

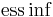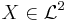
If $D(X) < \mathbb{E}[X] - \operatorname{ess\inf} X$ for every X (where $\operatorname{ess\inf}$ is the essential infimum) is a deviation risk measure, then there is a one-to-one relationship between D and an expectation-bounded coherent risk measure $\rho$ where for any $X \in \mathcal{L}^2$

$D(X) = R(X - \mathbb{E}[X])$
$R(X) = D(X) - \mathbb{E}[X]$ .

$\rho$ is expectation bounded if $\rho(X) > \mathbb{E}[-X]$ for any nonconstant X and $\rho(X) = \mathbb{E}[-X]$ for any constant X.^[7]

References

^ Artzner, Philippe; Delbaen, Freddy; Eber, Jean-Marc; Heath, David (1999). "Coherent Measures of Risk" (pdf). Mathematical Finance 9 (3): 203–228. http://www.math.ethz.ch/~delbaen/ftp/preprints/CoherentMF.pdf. Retrieved February 3, 2011.
^ Wilmott, P. (2006). Quantitative Finance. 1 (2 ed.). Wiley. p. 342.
^ Föllmer, H.; Schied, A. (2002). "Convex measures of risk and trading constraints". Finance and Stochastics 6 (4): 429–447.
^ Jouini, Elyes; Meddeb, Moncef; Touzi, Nizar (2004). "Vector–valued coherent risk measures". Finance and Stochastics 8 (4): 531–552.
^ Hamel, Andreas; Heyde, Frank (December 11, 2008) (pdf). Duality for Set-Valued Risk Measures. http://www.princeton.edu/~ahamel/SetRiskHamHey.pdf. Retrieved July 22, 2010.
^ Föllmer, Hans; Schied, Alexander (2004). Stochastic finance: an introduction in discrete time (2 ed.). Walter de Gruyter. ISBN 9783110183467.
^ Rockafellar, Tyrrell; Uryasev, Stanislav; Zabarankin, Michael (2002) (pdf). Deviation Measures in Risk Analysis and Optimization. http://www.ise.ufl.edu/uryasev/Deviation_measures_wp.pdf. Retrieved October 13, 2011. }}

External links

A list of important papers on coherent and convex risk measures
Glyn Holton: The Case for Incoherence Controversial article that argues coherence is not a desirable property. "There are two types of risk metrics – coherent and incoherent. In the vast majority of cases, you want one that is incoherent."

Coherent risk measure

Contents

Properties

Convex risk measures

Examples

Value at risk

Illustration

Average value at risk

Tail value at risk

Entropic risk measure

Superhedging price

Set-valued

Properties

Set-valued convex risk measure

Relation to Acceptance Sets

Risk Measure to Acceptance Set

Acceptance Set to Risk Measure

Dual representation

Relation to deviation risk measure

References

External links

See also